Token Ring Protocol in TLA+: Part 1

Published

October 20, 2024

What is a Token Ring? It’s simply a network where computers are arranged in a ring, and they pass a special “token” around. Only the computer holding the token can send data. It’s like a game of hot potato, but with data.

Token Ring Network


2. TLA+ Environment Setup

Before we start modeling, we need to set up our TLA+ environment. If you haven’t already, go ahead and download the TLA+ Toolbox. It’s like an IDE for TLA+.

Once you’ve installed the TLA+ Toolbox, create a new specification. Let’s call it TokenRing:

---- MODULE TokenRing ----
EXTENDS Naturals, Sequences

CONSTANT N

ASSUME N > 0

\* We'll add more stuff here soon!

====
Little note

At this time of writing, TLA+ syntax highlighting is not supported by the library I use here. I have created an initial Merge Request for it, and it’s been merged (also, this one); I’m waiting for it to be released.

In our spec, we’re creating a module called TokenRing. We’re also importing the Naturals and Sequences modules - they’re built-in and provide tools to work with numbers and sequences.

We’ve defined a constant N - this is the number of nodes in our ring. The ASSUME statement is like a sanity check - we’re saying N should be positive, because a ring with zero or negative nodes doesn’t make sense.

3. Modeling the Basics: Nodes and Token

Now, let’s model the basic components of our Token Ring: the nodes and the token.

---- MODULE TokenRing ----
EXTENDS Naturals, Sequences

CONSTANT N

ASSUME N > 0

Nodes == 1..N

VARIABLE token

TypeOK == token \in Nodes

Init == token = 1

Next == token' = IF token = N THEN 1 ELSE token + 1

Spec == Init /\ [][Next]_<<token>>

====
1
Nodes == 1..N: This defines our set of nodes. If N is 3, Nodes would be {1, 2, 3}.
2
VARIABLE token: This declares our token. It’ll represent which node currently has the token.
3
TypeOK: This is a type invariant. It says the token should always be a valid node number.
4
Init: This is our initial state. We’re starting with Node 1 having the token.
5
Next: This defines how our system changes. The token moves to the next node, or back to 1 if it was at N.
6
Spec: This puts it all together, saying our system starts in the Init state and then follows the Next action.

I configured N = 5 then ran this spec in the TLA+ Toolbox:

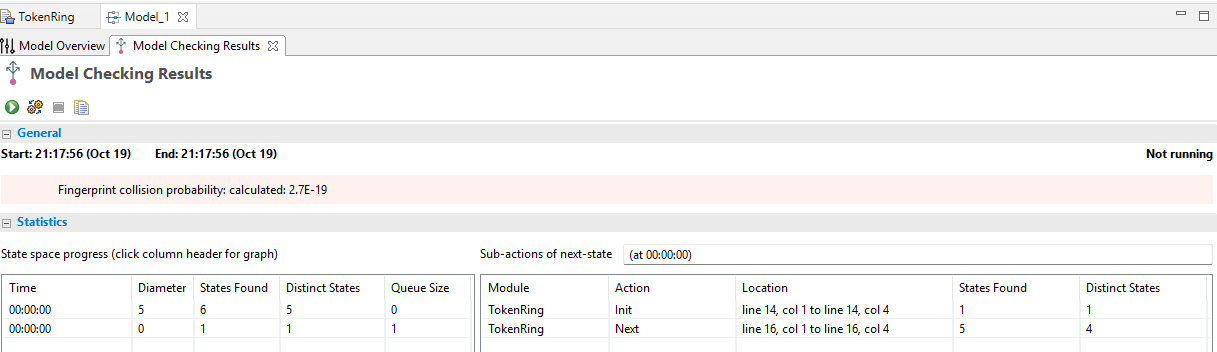
Token Ring Model Checking Results in TLC

These rows show how the model checker progressed from the initial state to fully exploring all possible states of the system. The final results (5 distinct states) align with what we’d expect from a token ring system, where the token can be in five different positions (given N=5 in this case).

4. Implementing Token Passing

Now that we’ve got the basic token movement, let’s make our nodes actually do something when they have the token. We’ll have them set a flag when they’re active (i.e., have the token).

---- MODULE TokenRing ----
EXTENDS Naturals, Sequences

CONSTANT N

ASSUME N > 0

Nodes == 1..N

VARIABLES token, active

TypeOK == 
    /\ token \in Nodes
    /\ active \in [Nodes -> BOOLEAN]

Init == 
    /\ token = 1
    /\ active = [n \in Nodes |-> IF n = 1 THEN TRUE ELSE FALSE]

PassToken ==
    /\ active[token]
    /\ active' = [active EXCEPT ![token] = FALSE]
    /\ token' = IF token = N THEN 1 ELSE token + 1
    /\ active' = [active' EXCEPT ![token'] = TRUE]

Next == PassToken

Spec == Init /\ [][Next]_<<token, active>>

====

At first glance, this specification looks reasonable (and perhaps deceptively simple). We initialize the system with the first node active and holding the token. The PassToken action seems to correctly pass the token and update the active status. However, when I ran this:

TLC reached a deadlock: 
Deadlock reached.
/\  active = <<TRUE, FALSE, FALSE, FALSE, FALSE>>
/\  token = 1
1
This is the TLC error that was thrown
2
This is the Error-Trace provided by TLC (it’s helpful for debugging as it helps understand states transitions, etc)

The TLA spec above seemed correct to me, but when the Deadlock error was thrown, I was in shock.

What did I do wrong? Why does this specification lead to a deadlock?

In TLA+, actions are atomic1 2. This means that everything described in an action happens instantaneously, as a single, indivisible step. There’s no concept of “first do this, then do that” within a single action. This atomicity is a fundamental principle in TLA+ and helps us reason about our systems at a certain level of abstraction.

In our initial state, Node 1 had the token and is active. The PassToken action looked like this:

PassToken == /\ active[token]
             /\ active' = [active EXCEPT ![token] = FALSE]
             /\ token' = IF token = N THEN 1 ELSE token + 1
             /\ active' = [active EXCEPT ![token'] = TRUE]
Tip

In TLA+, when we define an action like this, we’re describing a relationship between the current state and the next state. The action is saying, “Here’s how the next state should relate to the current state.”

Let’s think about this deadlock in terms of a light switch. Let’s say we have a special light switch with a rule:

You can only flip this switch if the light is currently on, and flipping it will turn the light off.

Now, let’s parallel this with our TLA+ action:

PassToken ==
    /\ active[token]  \* The light must be on to flip the switch
    /\ active' = [active EXCEPT ![token] = FALSE]  \* Flipping the switch turns the light off
    \* etc...

Here’s the problem: Once you flip the switch to turn the light off, you can never flip it again. Why? Because the rule states you can only flip it when the light is on, but flipping it always turns the light off.

That’s it! This is the deadlock: a state where the system halts and cannot evolve anymore.

In our TLA+ spec:

  • The light being on is like active[token] being TRUE
  • Flipping the switch is like executing the PassToken action
  • The light being off after flipping is like active[token] being FALSE in the next state

Just as you can only flip the switch once before getting stuck, our TLA+ spec can only execute the PassToken action once before reaching a deadlock.

This is why splitting into two actions solves the problem. It’s like changing our rule to:

  1. You can flip the switch off if the light is on
  2. You can flip the switch on if the light is off

Now we can keep flipping the switch back and forth, just like our adjusted TLA+ spec can keep passing the token:

---- MODULE TokenRing ----
EXTENDS Naturals, Sequences

CONSTANT N

ASSUME N > 0

Nodes == 1..N

VARIABLES token, active

TypeOK == 
    /\ token \in Nodes
    /\ active \in [Nodes -> BOOLEAN]

Init == 
    /\ token = 1
    /\ active = [n \in Nodes |-> IF n = 1 THEN TRUE ELSE FALSE]

DeactivateNode ==
    /\ active[token]
    /\ active' = [active EXCEPT ![token] = FALSE]
    /\ UNCHANGED token

ActivateNextNode ==
    /\ ~active[token]
    /\ token' = IF token = N THEN 1 ELSE token + 1
    /\ active' = [active EXCEPT ![token'] = TRUE]

Next == DeactivateNode \/ ActivateNextNode

Spec == Init /\ [][Next]_<<token, active>>

====
In this new version:
  1. We’ve split PassToken into two separate actions: DeactivateNode and ActivateNextNode.
  2. DeactivateNode turns off the active flag for the current token holder.
  3. ActivateNextNode moves the token to the next node and activates it, but only if the current token holder is not active.
  4. Our Next action is now the disjunction of these two actions, allowing either to happen in each step.

Our system now accepts an intermediate state where the current node is inactive but the token hasn’t moved yet. Each of these actions is still atomic, but we’ve changed the granularity of our model to better reflect the actual process of passing a token.

Alright, well, now let’s model check our spec:

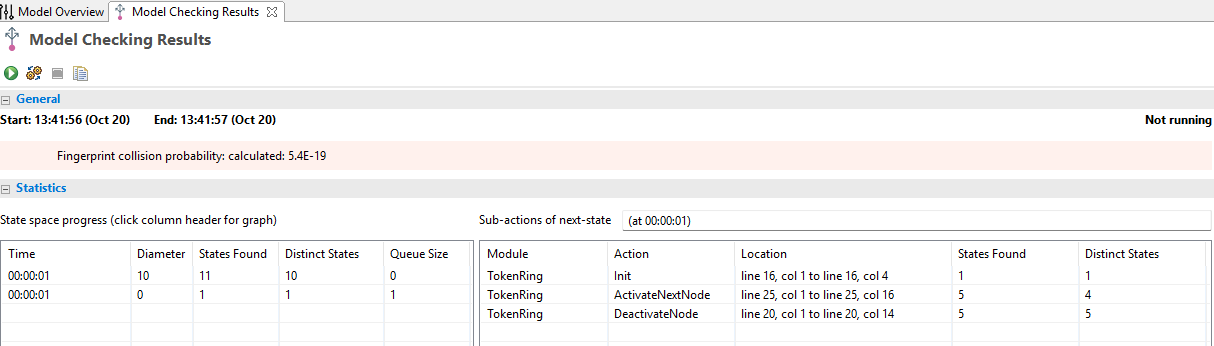
Model Checking our Token Ring TLA+ Spec

As you can see, this specification correctly models the token-passing process without deadlocks. When I ran it in TLC, the system continued to evolve, with the token moving around the ring and nodes activating and deactivating as expected.

This situation shows an important point in TLA+ modeling: the level of atomicity we pick can really affect how our specification behaves. Sometimes, what we conceptualize as a single operation in our mental model of a system actually needs to be broken down into multiple atomic steps in our TLA+ specification.

5. Adding Data Transmission

Now that we have a working basic token passing system, we should add the data transmission ability to our system.

First, let’s extend our constants and variables:

CONSTANT N, Data, NULL

ASSUME N > 0

Nodes == 1..N

VARIABLES token, active, messages, buffer

We’ve added Data to represent the set of possible messages, and NULL as a constant to represent the absence of a message. We also introduce two new variables: messages for queues of messages and buffer for the current message being processed.

Let’s update our type invariant and initial state:

TypeOK == 
    /\ token \in Nodes
    /\ active \in [Nodes -> BOOLEAN]
    /\ messages \in [Nodes -> Seq(Data)]
    /\ buffer \in [Nodes -> Data \union {NULL}]

Init == 
    /\ token = 1
    /\ active = [n \in Nodes |-> IF n = 1 THEN TRUE ELSE FALSE]
    /\ messages = [n \in Nodes |-> << >>]
    /\ buffer = [n \in Nodes |-> NULL]

Now, let’s add the ability to send messages. We’ll create a new action SendMessage:

SendMessage(n) ==
    /\ active[n]
    /\ buffer[n] = NULL
    /\ \E d \in Data:
        /\ messages' = [messages EXCEPT ![n] = Append(@, d)]
        /\ UNCHANGED <<token, active, buffer>>

This action ensures that an active node with an empty buffer adds a new message to its message queue, without changing anything else in the system.

Next, let’s add the ability to receive messages with a ReceiveMessage action:

ReceiveMessage(n) ==
    /\ active[n]
    /\ buffer[n] = NULL
    /\ messages[n] # << >>
    /\ buffer' = [buffer EXCEPT ![n] = Head(messages[n])]
    /\ messages' = [messages EXCEPT ![n] = Tail(@)]
    /\ UNCHANGED <<token, active>>

The ReceiveMessage action ensures that an active node with an empty buffer moves the first message from its message queue into its buffer, removing that message from the queue while keeping the token position and node activation status unchanged.

Then, we update our ActivateNextNode and DeactivateNode actions:

ActivateNextNode ==
    /\ ~active[token]
    /\ token' = IF token = N THEN 1 ELSE token + 1
    /\ active' = [active EXCEPT ![token'] = TRUE]
    /\ buffer' = [buffer EXCEPT ![token'] = NULL]
    /\ UNCHANGED messages

DeactivateNode ==
    /\ active[token]
    /\ active' = [active EXCEPT ![token] = FALSE]
    /\ UNCHANGED <<token, messages, buffer>>

Finally, let’s update our Next action to include these new features for our system:

Next ==
    \/ \E n \in Nodes: 
        /\ active[n]
        /\ (SendMessage(n) \/ ReceiveMessage(n))
    \/ DeactivateNode
    \/ ActivateNextNode

Awesome! So, I ran TLC on this spec, with this setup:

  • N = 2
  • Data = {1}
  • NULL = NULL

… then waited 😴, and waited some more 💤… (Yes, I’m using emojis—it feels odd with TLA+!), and 30 minutes later, when I got back to my screen, here’s what I found:

Space Explosion in a TLA+ spec

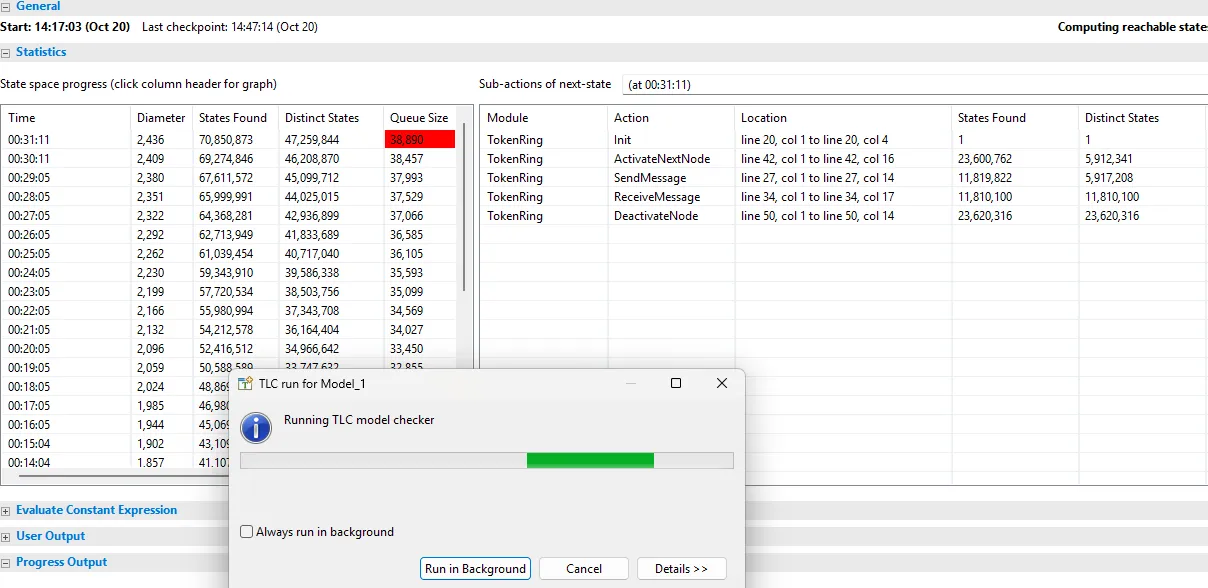
You guessed it. I had to cancel.

I realized that I have unbounded message sequences. Basically, the messages variable accepts an unlimited number of messages to be queued at each node. This is the cause of the state space explosion.

So, I introduced a constant MaxLength to limit the length of sequences in messages. I also modified the SendMessage action to make sure a message can only be sent if the sequence length is less than MaxLength.

Then, I ran the TLC model checker with this setup this time:

  • N = 3
  • NULL = NULL
  • Data = {1, 2, 3}
  • MaxLength = 2

And in less than 10 seconds… Tada!

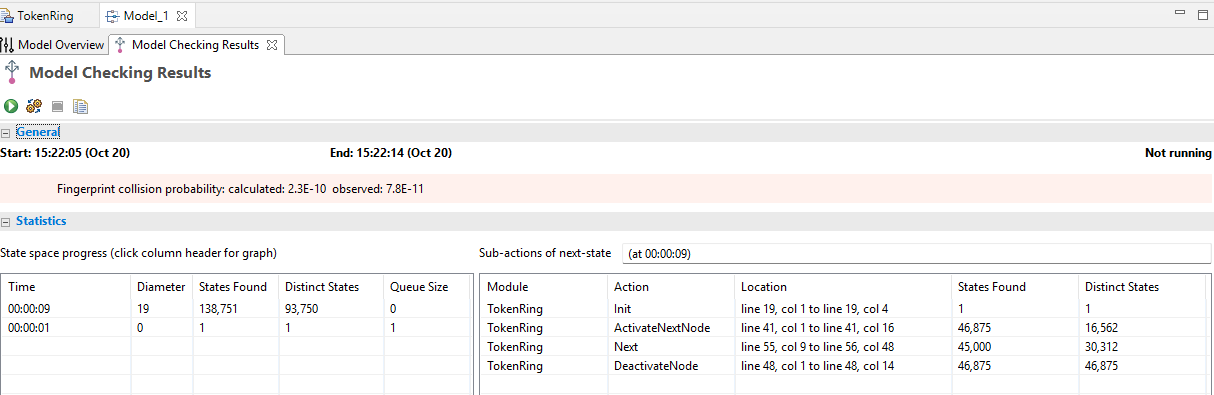
Token Ring Spec: TLC Model Checker Results

This TLA+ spec is hosted as a gist on Github:

6. Verifying Our Specification

The spec includes data transmission behavior now. However, we haven’t yet verified that it behaves correctly. We can use TLA+ to express the properties that our Token Ring Protocol should obey.

We’ve already defined TypeOK for type correctness. But we can also define a property that ensures the token keeps moving and eventually reaches every node. We could also have a property that ensures, at any given time, only one node can hold the token.

We’ve learned quite a bit up to this point. Let’s save the verification of these properties for next time!

Happy specifying!

Footnotes

  1. The Temporal Logic of Actions - Leslie Lamport↩︎

  2. In this TLA+ discussion thread, users debate the trade-offs between modeling message passing as atomic actions versus separate send and receive steps in a distributed system↩︎